Zombies de crecimiento exponencial

Anoche pusieron en televisión Guerra Mundial Z. En 2013 Brad Pitt decidió producir esta película encargando su dirección a Marc Foster (director de Cometas en el cielo, Quantum of Solace, y la ya mencionada en nuestro blog Mas extraño que la ficción). Brad Pitt, que además es el protagonista de la película, aprovechaba de esta forma el boom de temática zombie ocasionado especialmente tras el estreno de la serie The Walking Dead.

La principal diferencia de esta película, frente al resto de películas sobre un apocalipsis zombie (tema muy recurrido en Hollywood a lo largo de su historia), es que los zombies de Guerra Mundial Z son capaces de interactuar entre ellos para conseguir un objetivo, trabajando de forma conjunta - como hacen, por ejemplo, las hormigas -. Lo podemos ver al final de su trailer:

¿Y que tienen que ver las matemáticas con los zombies? Pues bien, las matemáticas nos explican el modelo de crecimiento que tiene la cantidad de zombies existente. Como vemos en la película, el número de afectados crece de forma muy rápida:

Además, más tarde sabremos que los primeros indicios de este virus provienen de sólo 11 días antes en Sudáfrica:

¿Qué modelo explica este crecimiento? A este tipo de comportamiento lo llamamos crecimiento exponencial. Para entenderlo partamos de un ejemplo. Supongamos que existe una persona infectada, y que este zombie contagia a una sola persona al día. De esta forma el número de zombies crecería de la siguiente forma:

Es decir, al irse doblando el número de zombies día a día, inicialmente no trabajaremos con grandes números pero en sólo 35 días el número de zombies alcanzaría los 8.589.934.592 infectados. La población mundial!!. Gráficamente lo representaríamos con la siguiente función:

Aquí tenéis de nuevo el planteamiento (en inglés):

Ahora bien, ¿qué ocurriría si en vez de contagiar a una persona al día lo hiciera con más? En ese caso el crecimiento sería mucho mayor, pues el número de infectados en lugar de doblarse se iría multiplicando por ese número provocando un crecimiento mucho más rápido y una función mucho más inclinada.

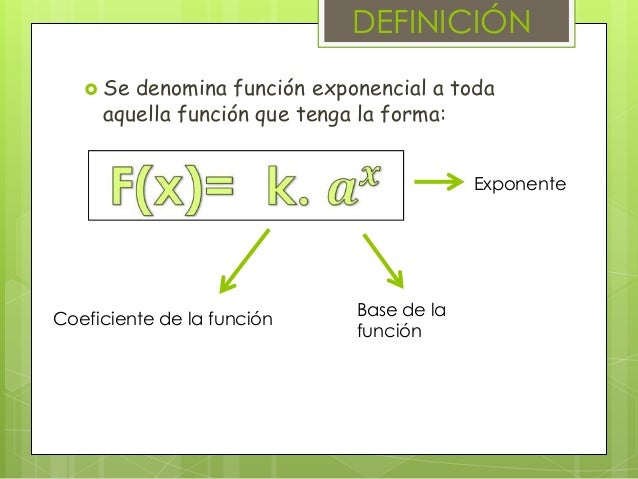
Expresar este crecimiento en forma de una función, llamada función exponencial, nos permite realizar cálculos y "pronosticar" el número de afectados tras x días. Y al revés, el conocimiento de la fórmula que explica este crecimiento nos permite despejar cualquier incógnita de esta ecuación exponencial. 

La fórmula de esta función dependerá del números de afectados inicialmente (en el momento x=0), del tiempo (x) y de la constante de crecimiento (el número por el que se multiplica los casos). Esta constante estará en forma de potencia, elevada al tiempo.

Para el caso de los Guerra Mundial Zeta, la base de la función sería el número de infectados por zombie al día, x el número de días. Con los datos de infectados que da la película tras 11 días, podríamos despejar y decir que cada zombie ataca a más de siete vivos al día. Ya que:

• Tras 11 días hay aproximadamente 3200 billones de infectados (billones de los américanos supongo)
• Por tanto la base (a) elevada a 11 debe dar 3200000000
• Al despejar realizamos la raíz de indice 11 de 3200000000 obteniendo 7,313.

Al margen del uso en la ficción para ver el número de zombies, la función exponencial es utilizada en la vida real en casos como el crecimiento de bacterias en un cultivo, el tiempo que toma un objeto para alcanzar una temperatura, progresión de un virus en un cuerpo, termodinámica.

La función exponencial no sólo explica crecimientos también decrecimientos. Dependerá de la base de la función. De esta forma si la base de la función es mayor que 1 se producirá un crecimiento (mayor conforme sea la base), pero si la base es menor que 1 (y mayor que 0) la función será cada vez menor.

Entonces, tras poder controlar el virus, una función de base menor que 1 podría llagar explicarnos cómo el número de afectados disminuye con el paso del tiempo.

Por último indicar que no tendría sentido de hablar de una base menor que cero (por tanto negativa), ya que su función serían puntos aislados que irían alternando su signo.

• ¿Has visto la película? ¿Qué te parece? Que sepas que pronto estrenarán la segunda parte.
• ¿Conocías la función exponencial? Busca información de otros casos de la vida real en los que se utiliza esta función.
• Por último, ¿Estás preparado para un apocalipsis zombie? ¿Conoces gente que está involucrada en esta moda?

Te animamos a comentar este post y/o a participar tratando cualquier otra película. Puedes escribir a cinemaths@gmail.com