Spiderman, un as en Geometría

 

"Spider-Man: Lejos de casa" (2019) es la segunda entrega de la trilogía de Spider-Man dirigida por Jon Watts, que sigue a Peter Parker, interpretado por Tom Holland. La película también cuenta con actuaciones destacadas de Zendaya, Jake Gyllenhaal, Samuel L. Jackson y Marisa Tomei. La historia comienza después de los eventos de "Avengers: Endgame", con Peter Parker tratando de llevar una vida normal después de la pérdida de su mentor, Tony Stark. Durante un viaje escolar a Europa, Peter se encuentra con Mysterio, interpretado por Jake Gyllenhaal, un supuesto superhéroe de otra dimensión. Pronto descubre que las cosas no son lo que parecen y debe enfrentarse a nuevas amenazas mientras intenta proteger a sus amigos y asumir su responsabilidad como Spider-Man. Aquí puedes ver el trailer:

La película recoge varios momentos que podemos relacionar con las matemáticas. Por ejemplo, en el minuto 10 de la película, Peter Parker lleva una camiseta con un ingenioso problema matemático:

La camiseta muestra un triángulo rectángulo con los catetos etiquetados y la instrucción "Find x" (encuentra x). La solución está humorísticamente escrita en rojo, rodeando la "x" y añadiendo "I found it" (la encontré). Esta broma matemática hace referencia al Teorema de Pitágoras, que establece que en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de los cuadrados de los otros dos lados. Matemáticamente, esto se expresa como:

donde  a  y  b son los catetos y c es la hipotenusa. Este teorema es fundamental en geometría y tiene aplicaciones en diversas áreas como la construcción, la navegación y la física.

.

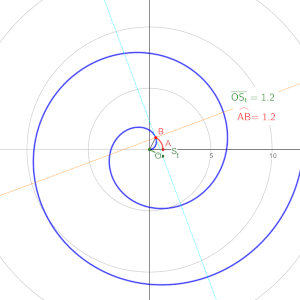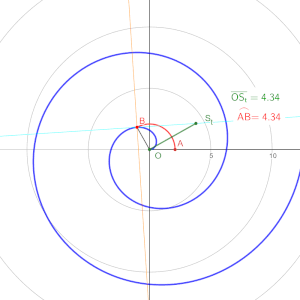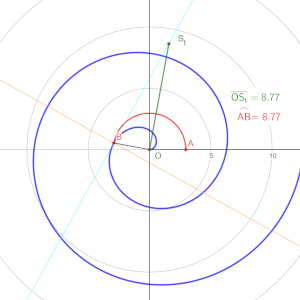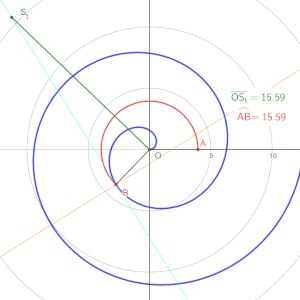
Avanzando en la película, alrededor del minuto 59, Spider-Man se encuentra persiguiendo al Dr. Strange en la dimensión espejo, un entorno surrealista donde las leyes de la física parecen estar distorsionadas. En medio de la persecución, Peter reconoce una espiral de Arquímedes y se da cuenta de que la dimensión espejo está basada en geometría pura. Reflexiona: "Un momento, ¿eso es una espiral de Arquímedes? ¿La dimensión espejo solo es geometría pura? Tú eres un as de la geometría. Usa la geometría". Luego continúa: "Eleva el radio al cuadrado, divídelo por pi, catapultas a lo largo de la curva".

La espiral de Arquímedes es una curva que se define por la ecuación  r = a + b\theta, donde r  es el radio y \( \theta \) es el ángulo. En la vida real, las espirales de Arquímedes se pueden observar en la naturaleza, como en las conchas de ciertos moluscos y en la disposición de las semillas de girasol. Estas espirales también tienen aplicaciones prácticas en la ingeniería y la tecnología, por ejemplo, en el diseño de antenas, engranajes y bombas de agua.

Finalmente, durante los créditos finales de la película, suena la canción "Three is a Magic Number" de De La Soul. Esta canción celebra el número tres y sus propiedades únicas. La letra destaca cómo el número tres aparece en varios contextos significativos y culturales. Matemáticamente, el número tres es especial por varias razones: es el primer número primo impar, es un número triangular y es parte de la secuencia Fibonacci. Además, el tres tiene una presencia importante en la religión, la literatura y la simbología, a menudo asociado con conceptos de equilibrio y armonía. 

Durante los créditos, los espectadores pueden ver diversos elementos matemáticos representados como dibujos de cómics, lo que añade un toque educativo y visualmente atractivo al cierre de la película. Algunos ejemplos de esos elementos son:

•  El triángulo de Penrose:

Es una figura imposible, un objeto que no puede existir en el espacio tridimensional, aunque su representación bidimensional parece real. Cada esquina del triángulo de Penrose parece estar conectada de una manera que desafía la lógica, creando una ilusión óptica que hace que el triángulo parezca perfectamente normal a primera vista, pero imposible cuando se observa más detenidamente.

•  Un triángulo medial:

Un triángulo formado por los puntos medios de los lados de otro triángulo. El triángulo medial tiene propiedades interesantes; es similar al triángulo original y su área es exactamente la mitad del área del triángulo original. Además, sus lados son paralelos a los lados del triángulo original.

•  Escaleras imposibles tipo Escher:

Escaleras que parecen continuar indefinidamente en una dirección, creando un bucle infinito. Popularizadas por el artista M.C. Escher, estas escaleras representan una paradoja visual donde cada segmento parece lógicamente correcto, pero en conjunto, forman una estructura imposible.

•  Espiral Arquimediana:

Una espiral matemática en la que la distancia entre giros sucesivos es constante. Es común en la naturaleza y la ingeniería, apareciendo en fenómenos como las bobinas de los relojes y las caracolas.

•  Espiral de Fibonacci:

Una espiral que se aproxima a la espiral dorada y se forma mediante cuadrados cuyas longitudes de lado corresponden a los números de Fibonacci. La secuencia de Fibonacci se define como una serie donde cada número es la suma de los dos anteriores (0,1,1,2,3,5,8,...0, 1, 1, 2, 3, 5, 8, ...0,1,1,2,3,5,8,...). Esta espiral aparece frecuentemente en la naturaleza, como en las conchas de nautilus, los girasoles y las piñas.

Otras muchas figuras matemáticas:

"Spider-Man: Lejos de casa" combina acción, humor y referencias intelectuales, utilizando conceptos matemáticos de manera creativa para enriquecer la narrativa y desarrollar el carácter de Peter Parker. Desde la camiseta humorística hasta la aplicación de la geometría en situaciones de alta tensión, la película demuestra cómo las matemáticas pueden ser tanto una herramienta práctica como una fuente de entretenimiento.

Viaja en el tiempo con los Vengadores

Para sorpresa de todos Vengadores: Infinity War (Anthony y Joe Russo, 2018) nos dejaba helados con un final en el que el todopoderoso Thanos conseguía acabar con la mitad del universo, incluyendo superhéroes como Spiderman, Black Panther, Doctor Extraño, Starlord, Groot... (mira la imagen de abajo para repasar quiénes sabemos quedaban vivos y quienes no tras Infinity War). Tras este final parecía obvio que esto no podía quedar así y que de alguna manera en la secuela Vengadores: Endgame (Anthony y Jose Russo, 2019) nos los traería de vuelta. Pero, ¿cómo sería?

Pongámonos en situación de cómo nos dejó Infinity War y qué esperabamos de Endgame viendo el trailer:

"El mundo ha cambiado tanto y no se puede volver atrás" y "A veces lo mejor que podemos hacer es volver a empezar" son frases que, junto con otros detalles del trailer, sirvieron de base para distintas teorías que hacían suponer que la clave estaba en los viajes en el tiempo. Y, perdón por este pequeño spoiler, así es.

Y, ¿cómo conseguir viajar en el tiempo? Es fácil adivinar que si alguien es capaz desarrollar una tecnología para ello debía ser Tony Stark, quién tras muchas dificultades conseguirá la clave para dichos viajes. Y, posiblemente te pasó desapercibida, pero esa clave tiene mucho que ver con las matemáticas. Veámoslo en esta escena:

Tras muchos intentos y ya casi a la desesperada, Tony manda hacer una simulación con la forma de una cinta de Moebius.  Pero ¿sabes qué forma es esa? y ¿quién fue Moebius?

Crear una banda de Moebius es sencillo, basta con tomar una tira de papel y pegar sus extremos girando antes uno de ellos 180 grados. La figura resultante tiene unas particularidades sorprendentes: Posee una única cara y un único borde. Para comprobarlo, basta con recorrer con un dedo el borde de la cinta, hasta comprobar que se ha recorrido todo sin levantarlo en ningún momento, y por ejemplo, pasar un lápiz por la cara de la banda, comprobando que al regresar al punto de partida, las supuestas dos caras del objeto han quedado marcadas. Esto quiere decir que no podemos hablar de parte de arriba o de abajo, pues es un objeto no orientable. Si no lo has entendido por escrito seguramente este video te lo deje más claro (y además verás algunas aplicaciones)

¿Qué más tiene de especial esta figura? Se utiliza en campos tan dispares como la Matemática, el Arte, la Ingeniería, la Ciencia, la Arquitectura, la Música, el Diseño, la Literatura, etc., ya sea de manera explícita o como una metáfora. Simboliza especialmente el infinito y la naturaleza cíclica por eso su representación del reciclado.

¿Y por qué esta forma en los Vengadores? Pues deberíamos preguntárselo a los guionistas pero aquí van nuestras teorías:
- La banda de Moebius se asocia al infinito y con ella recuperamos a los superhéroes muertos en Infinity War, por las joyas del infinito.
- La banda de Moebius se asocia también a la continuidad, algo que preocupa normalmente en los viajes en el tiempo.
- También se asocia a los ciclos, y con Vengadores: Endgame está claro que acabamos un ciclo para empezar uno nuevo (está vez no haremos spoiler del final pero está claro que las cosas han cambiado definitivamente para algunos superhéroes).

¿Y quién fue Moebius? Fue un matemático alemán conocido especialmente por la banda de con su nombre, pero además desarrolló la transformación de Möbius, importante en geometría proyectiva y  la transformada de Möbius, usada en teoría de números.

• ¿Has visto Vengadores: Endgame? ¿Qué te parece?
• ¿Observaste que hacía referencia a la banda de Moebius? ¿La conocías?
• ¿Cual de nuestras teorías te parece más acertada?

Por último os dejamos este mapa de viajes en el tiempo de Engame:

La Binomial de Spiderman

La supremacía de Disney - Pixar sobre el resto de productoras de animación queda demostrada por la taquilla y los premios. Desde que en 2002 se introdujera el premio a mejor película de animación en pocas ocasiones el galardón ha ido a otra productora Las pocas excepciones (Shrek, El viaje de Chihiro, Wallace & Gromit, Happy Feet y Rango) coinciden con años en los que Disney no ha lanzado ninguna película o ha sido una película menor (ej. Lilo & Stich). Lo mismo ocurre si analizamos  los ganadores de los premios Annie (Asociación Internacional de Películas Animadas). Sin embargo este año una película se imponía con creces a sus grandes apuestas cómo la esperada Los increíbles 2 o Ralph rompe internet, (e incluso Isla de perros de Wes Anderson) consiguiendo, además del galardón  el aplauso de público y crítica. Hablamos de Spiderman: Un nuevo universo.

¿Cómo a estas alturas una película de Spiderman consigue tener este éxito? La respuesta está por un lado en su estética (muy inspirada en el mundo del comic) y un argumento que une acción con dosis de humor. A falta de un Spiderman, en esta película el protagonista Miles Morales, un adolescente afroamericano, se encontrará con sus similares en universos paralelos muy distintos: el conocido Peter Parker, Spider-Gwen una versión femenina, Spider-Man su alter-ego en cine negro, Peni Parker versión manga futurista e incluso Spider-cerdo. Conócelos en este trailer:

Centrándonos en el protagonista, Miles Morales es un adolescente de Brooklyn que acaba de acceder a un prestigioso instituto privado, aunque el preferiría quedarse con sus amigos de siempre en su anterior centro. Eso le llevará a la siguiente escena que vamos a tratar:

Comencemos, aunque sea algo más anecdótico por observar la pizarra de clase y ver qué están estudiando:

Tanto a la izquierda del todo como sobre la cabeza de la profesora vemos que están trabajando integrales o primitivas, mientras que a la derecha lo que vemos es algún tipo de ecuación con raíces; es decir unas matemáticas bastante avanzadas sobretodo sabiendo que en teoría Miles tiene 13 años... En teoría a esa edad debería estar en 8º grado del sistema educativo americano, donde ven poco más de ecuaciones lineales y sistemas de ecuaciones. Así que o es una escuela de alto rendimiento o se han colado un poco con lo de la pizarra...

Por otro lado, si analizamos lo que ocurre en la escena, Miles acaba de sacar un 0 sobre 100, lo cual hace sospechar a la profesora ya que esta nota es muy improbable. ¿Por qué? Empecemos por definir lo que es una experiencia dicotómica: aquella que tiene solo dos resultados posibles (como el examen de Miles que es de Verdadero - Falso). Entendiendo que Miles contestara a una pregunta al azar tendría una probabilidad de 1/2 (o 50% como se suele decir) de acertar la respuesta.

Supongamos también que este experimento se repite varias veces (las 100 preguntas del examen). El comportamiento de este experimento sigue una distribución probabilística llamada Distribución Binomial. Esta distribución nos permite calcular la probabilidad de un determinado número de éxitos sobre el total de veces que se repite el experimento de la siguiente forma:

Para el caso concreto del examen de Miles n = 100 pues son el número de preguntas del examen, y p y q son 0,5 (al tener las dos respuestas la misma probabilidad ya que contesta al azar). De esta forma la probabilidad de, por ejemplo, acertar 25 de las 100 preguntas sería:

Esta probabilidad es de 0,00000913139706451239

Lo bueno de la distribución binomial es la existencia de unas tablas por las que podemos obtener estas probabilidades sin necesidad de realizar los cálculos, lo cual es muy práctico. Estas tablas nos van dando cada probabilidad en función de n, p y x.

Ahora bien, la binomial nos da la probabilidad de éxito un determinado número de veces y no acumula probabilidades. Es decir nos dice cual es la probabilidad de que acierte 25 preguntas exactamente pero no 25 o menos, para lo cual tendríamos que ir sumando las probabilidades de que ocurra 1, 2, 3,... y hasta 25 veces.
Haciendo esto la probabilidad de acertar hasta 25 preguntas sería 0.00000281814101710270177  mientras que la de acertar 50 sería 0,5398 (se aproxima pero no es el 50% que decía Miles).

Además, P (X = 0), es decir, la probabilidad de fallar todas las preguntas es de 7.888609052210118·10^-31  así que normal que la profesora sospechara!!.

Debemos decir que la distribución binomial se puede aproximar a otra importante y conocida distribución de probabilidad: la distribución Normal. Esta aproximación la podemos hacer cuando tenemos una n grande, o mejor dicho cuando el producto de n por p es grande. La distribución Normal, a diferencia de la Binomial, sí nos da la probabilidad acumulada, y también tiene tablas que nos facilita tener que hacer los cálculos. De esta forma la probabilidad de que aprobar el examen, es decir de acertar al menos 50 preguntas sí que es exactamente de un 50%.

• ¿Qué te ha parecido este post? ¿Conocías estas distribuciones de probabilidad?
• ¿Has podido entender la distribución binomial? Piensa en casos en las que puede ser útil.
• Prueba a obtener probabilidades usando las tablas.
• ¿Conocías la película? ¿Qué te parece?

Como siempre te invitamos a opinar y a proponer películas para tratar en el blog.

•