Terminator 2: Judgment Day se estrenó en 1991 y fue dirigida por James Cameron, que ya había dirigido la primera entrega en 1984. La película cuenta con Arnold Schwarzenegger repitiendo su icónico papel como el cyborg Terminator, acompañado por Linda Hamilton como Sarah Connor, Edward Furlong como su hijo John Connor, y Robert Patrick como el implacable T-1000. La cinta fue un éxito absoluto tanto de taquilla como de crítica, y ganó cuatro premios Oscar en categorías técnicas: mejores efectos visuales, sonido, edición de sonido y maquillaje. Hoy sigue siendo un referente en el cine de ciencia ficción y acción.
La importancia de Terminator 2 va más allá de su espectacularidad. Supuso una revolución en los efectos especiales, especialmente con la tecnología del T-1000, y consolidó la saga como una de las más influyentes del género. La película se ha convertido en objeto de culto, gracias a sus icónicas frases, su crítica al desarrollo descontrolado de la inteligencia artificial, y su poderosa narrativa sobre el destino, la tecnología y la humanidad. Incluso más de treinta años después, sigue despertando debates sobre el futuro y la ética de las máquinas.
La historia nos sitúa unos años después de la primera película. Un nuevo Terminator es enviado al pasado con una misión: proteger al joven John Connor, futuro líder de la resistencia humana frente a las máquinas. Sarah Connor, su madre, se ha convertido en una guerrera decidida a impedir el juicio final: el día en que Skynet, una inteligencia artificial militar, tome conciencia de sí misma y provoque el exterminio nuclear de la humanidad. Juntos, intentarán detener la creación de Skynet antes de que sea demasiado tarde. Aquí el trailer:
Uno de los momentos más memorables de la película, desde una perspectiva matemática, ocurre pasados setenta y cinco minutos. El Terminator le explica a Sarah lo inevitable: “Se aprobará el presupuesto del Skynet. El sistema se conectará el 4 de agosto de 1997. Se eliminarán las decisiones humanas en la defensa estratégica. Skynet aprenderá en progresión geométrica. Tendrá conciencia de sí mismo a las 2 y 14 de la madrugada del 29 de agosto. Los humanos aterrados intentarán desconectarlo" Lo vemos aquí:
Nos centraremos en la frase, “aprenderá en progresión geométrica”, que es la que nos interesa analizar.
Recordemos qué es una progresión. En matemáticas, una progresión es una sucesión ordenada de números que siguen una regla específica. En el caso de las progresiones geométricas, cada término se obtiene multiplicando el anterior por una cantidad constante, llamada razón. Por ejemplo, en la sucesión 1, 2, 4, 8, 16,... la razón es 2, porque cada número es el doble del anterior.
Las progresiones geométricas tienen una característica muy interesante: crecen muy rápidamente si la razón es mayor que 1. En pocos pasos, los valores se disparan. Esto explica por qué en la película se utiliza esta expresión para describir el aprendizaje de Skynet. No aprenderá poco a poco, sino de forma acelerada, multiplicando su conocimiento de forma exponencial hasta volverse incontrolable. Es una forma muy cinematográfica (y bastante precisa) de sugerir que su evolución será veloz e imparable.
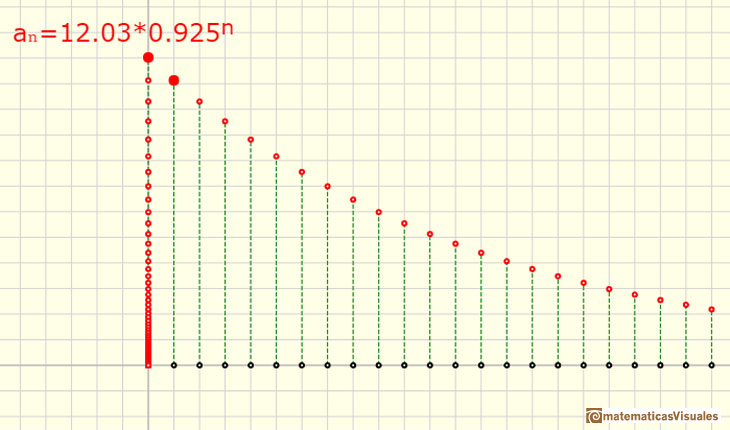
Pero cuidado: no todas las progresiones geométricas crecen. Si la razón está entre 0 y 1, los términos cada vez son más pequeños. Por ejemplo, en la sucesión 1, 0.5, 0.25, 0.125,... la razón es 0.5. En este caso, en lugar de crecer, los valores tienden a cero. Así que una progresión geométrica no siempre significa crecimiento, todo depende de la razón que se utilice.
Entendemos perfectamente lo que se quería transmitir en esa frase de la película: Skynet aprenderá tan rápido que los humanos no podrán seguirle el ritmo. La progresión geométrica es, en este contexto, una excelente metáfora del peligro del aprendizaje automático descontrolado. Pero como todo en matemáticas, conviene matizar y entender bien los conceptos. Porque cuando se trata del futuro... no hay que dejarlo todo en manos de las máquinas.