Destripando La Evasión

Hacía tiempo que no tratábamos en nuestro blog un clásico, y hoy lo hacemos por todo lo alto, una "obra maestra" según François Truffaut, y una de las mejores películas de la historia en múltiples rankings. Se trata de "La evasión" (Jacques Becker, 1960) un drama carcelario francés basado en hechos reales, que además de ser admirada por los expertos, tiene una puntuación media de 8,4 por los usuarios de filmaffinity.

Un nuevo interno llega a una celda donde otros cuatro presos planean escapar de prisión. Ese es el planteamiento inicial de la película, que destaca por su maestría en trasladar al espectador la sensación de claustrofobia de estar preso, el esfuerzo por intentar escapar y la camaradería entre los cinco presos.
No hemos encontrado un trailer en español, pero sí este vídeo que recoge algunos de sus mejores momentos:

Como hemos dicho, la película está basada en hechos reales. De hecho uno de los protagonistas se interpreta a sí mismo. Y es en esa dualidad realidad-ficción en la que nos vamos a basar para trabajar matemáticas.

Para escapar de prisión los protagonistas escavan un agujero (de ahí su título original Le trou - el agujero) que enlaza con los pasadizos subterráneos de la cárcel. Para orientarse realizan el siguiente plano:

Sin embargo, según vemos en Google Maps, la cárcel de la Santé en Paris, escenario real de la película, no tendría forma rectangular sino la siguiente:

¿ Reconoces qué forma poligonal tiene la prisión? Si nos centramos en la parte de la izquierda, que es dónde se desarrolla la acción, comprobamos que sigue manteniendo el mismo polígono, un trapecio. En cada uno de los cuatro vértices tendría un sótano, que están unidos por galerías.
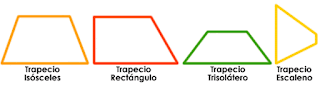
Pero es más, después de comprobarlo en los mapas de Google, podemos afirmar que se trata de un trapecio isósceles. ¿Recuerdas los tipos de trapecio?

Los presos inician la búsqueda del desagüe en su sótano, y no es hasta el tercero cuando lo encuentran, por lo tanto realizan el recorrido partiendo de A a D pasando por B y C, pero la vuelta la hacen directamente de D a A.

En concreto, de A a B, al igual que de C a D recorren 105 metros, y de B a C unos 60 metros. Con estos datos os planteamos el siguiente problema:
Problema, Atajando directamente de D a A se han ahorrado 170 metros. ¿Podrías decirnos cual es la superficie (área) que abarca la cárcel?

Una de las características de La Evasión es el manejo del tiempo en la misma. Podríamos dividir la película en dos partes, en la primera los prisioneros no tienen manera de controlar el tiempo y de igual forma el espectador, por ello el director utiliza largas tomas que nos indican lo complicado - y largo - que supone escapar de prisión. En la segunda parte, cuando los prisioneros ya tienen forma de calcular el tiempo, se utilizan otros métodos de indicar el tiempo transcurrido. Es, por tanto, clave el hecho de que los prisioneros se las apañen para cuantificar el tiempo. Veámos cómo lo logran:

• ¿Cómo de precisa te parece esta medida? ¿Crees que serías capaz de construir un reloj de arena? Y una vez creado, ¿cómo calcular el tiempo por primera vez?
• Suponemos que lo hace contando segundos, en ese caso ¿cuántos segundos habrá en media hora?

• ¿Has visto la película? ¿Qué te parece? ¿Crees se merece estar en el ranking de mejores películas de la historia?
• Comenta nuestro post, ¿hay algún otro tema de la película que crees que merece la pena ser tratado?
• Opina de este post o plantea otra película para que sea trabajada en nuestro blog.